Im ersten Teil dieser Artikelreihe haben wir uns mit den Grundlagen des Raytracings beschäftigt und Schnittstellen definiert, welche die einzelnen Softwarekomponenten bzw. ihre Funktionalität beschreiben. Wir werden im Folgenden eine der wichtigsten Komponente entwickeln: Die Kamera.

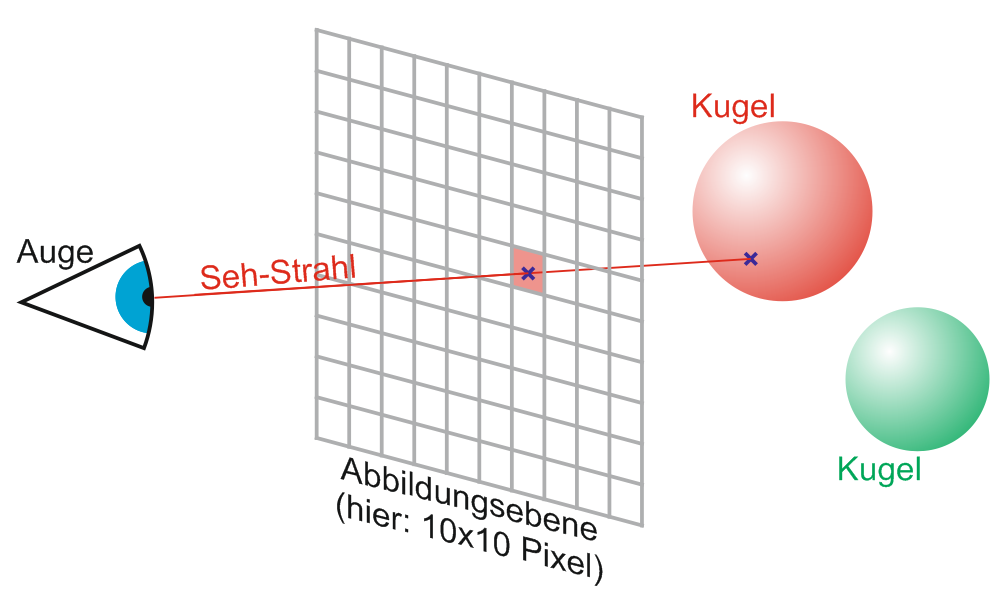
Aufgabe der Kamera ist es eine Bitmap-Grafik von einer Szene zu rendern. Sie sendet dazu für jeden Pixel einen Ray durch die Szene und ermittelt so, auf welches Primitiv der jeweilige Ray trifft. Der Pixel bekommt dann die Farbe des Primitivs. Weiterhin untersucht die Kamera die Ausrichtung der Fläche, auf der ein Ray endet, zum Licht und hellt den Pixel entsprechend auf, oder dunkelt ihn ab.

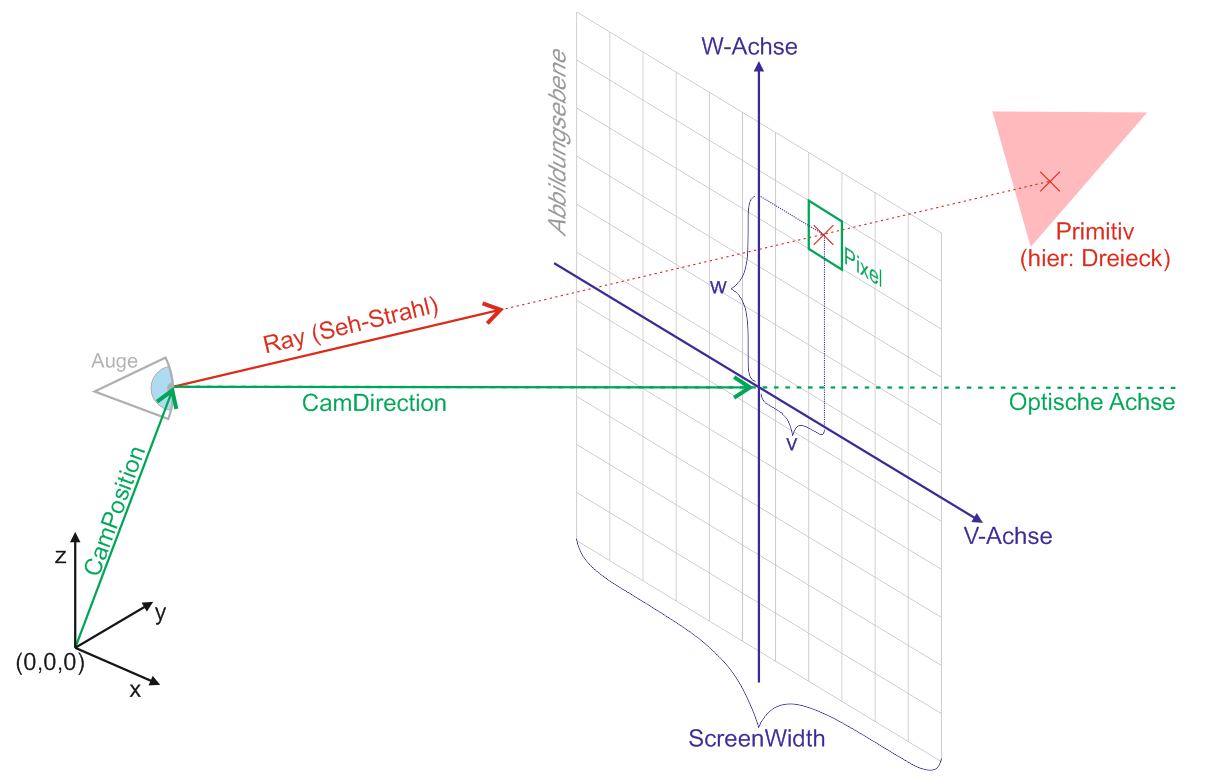
Eine Kamera hat eine Position im Raum, welche durch den Vektor CamPosition beschrieben wird. Weiterhin hat sie eine Blickrichtung, welche durch den Vektor CamDirection beschrieben wird. Die Länge des Vektors CamDirection entspricht dem Abstand der Abbildungsebene von der CamPosition. Um einer Verwechselungsgefahr mit dem dreidimensionalen Koordinatensystem x, y, z vorzubeugen, wollen wir die zweidimensionalen Koordinaten auf der Abbildungsebene nicht mit x und y sondern mit v und w bezeichnen. Die CamPosition befindet sich genau senkrecht über dem Nullpunkt (v=0, w=0) der Abbildungsebene. Eine Längeneinheit auf der Abbildungsebene entspricht genau einem Pixel. Der im Bild grün hervorgehobene Pixel hat also die Koordinaten (v=2, w=4). Da der Nullpunkt der Abbildungsebene hier genau in der Mitte des Bildes (und nicht wie sonst üblich in der oberen linken Ecke) liegt, können die Koordinaten eines Pixels auch negativ sein.

Die Klasse RayTraceCamera

Wir erstellen nun die Klasse RayTraceCamera. Im Konstruktor bekommt diese Klasse unter anderem ein IRayTraceable übergeben. Dies ist die Szene, in der sich alle Primitive befinden. Wie im vorhergehenden Teil beschrieben enthält das Interface IRayTraceable alle Methoden, die wir benötigen um die Szene mit Strahlen bzw. Rays zu untersuchen und daraus ein Bild zu rendern. Wie diese Methoden der Szene genau implementiert werden, soll uns an dieser Stelle zunächst egal sein. Weiterhin bekommt der Konstruktor der RayTraceCamera die Position und Blickrichtung der Kamera übergeben.

    public class RayTraceCamera
    {
        IRayTraceable scene;
        Vector3D camPosition;
        Vector3D camDirection; // Direction Vector with Length = eyeDistanceToScreen
        Vector3D camDirectionNorm; // Normalized Direction Vector
        Vector3D upDirection = Vector3D.eY; // Richtung nach oben 
        const double eyeDistanceToScreen = 1.5; // Abstand des Auges zur Abbildungsebene in Längeneinheiten des XYZ-Koordiantensystems
        const double screenWidth = 1; // Die Breite der Abbildungsebene in Längeneinheiten des XYZ-Koordiantensystems
        Vector3D eV; // Einheitsvektor in V-Richtung (horizontal) der Screen Ebene mit der Länge 1px
        Vector3D eW; // Einheitsvektor in W-Richtung (vertikal) der Screen Ebene mit der Länge 1px

        int screenWidthPx = 300;
        int screenHeightPx = 200;

        public RayTraceCamera(IRayTraceable scene, Vector3D camPosition, Vector3D camDirection)
        {
            this.scene = scene;
            MoveTo(camPosition, camDirection);
        }

        public void MoveTo(Vector3D position, Vector3D direction, Vector3D upDirection = null)
        {
            if (upDirection != null) this.upDirection = upDirection.normalize(); // wenn null, bleibt die upDirection unverändert
            camPosition = position;
            camDirectionNorm = direction.normalize();
            camDirection = camDirectionNorm * eyeDistanceToScreen; // direction-Länge auf eyeDistanceToScreen ändern
            Init();
        }

        public void ResizeScreen(int widthPx, int heightPx)
        { // Größe des gerenderten Bild in Pixeln setzen
            screenWidthPx = widthPx;
            screenHeightPx = heightPx;
            Init();
        }

        private void Init()
        {
            eV = camDirectionNorm.cross(this.upDirection);
            eW = eV.cross(camDirectionNorm);
            eV = eV * (screenWidth / screenWidthPx); // Länge auf 1px ändern
            eW = eW * (screenWidth / screenHeightPx); // Länge auf 1px ändern
        }
    }

Betrachten wir zunächst die Klassenvariablen: „scene“, „camPosition“ und „camDirection“ wurden bereits erwähnt und werden hier nicht weiter erläutert. Der Vektor „camDirectionNorm“ zeigt in die gleiche Richtung wie „camDirection“, er bekommt jedoch stets die Länge 1. Bisher haben wir nicht berücksichtigt, wie die Kamera seitlich geneigt ist (Rollwinkel). Um ein Bild zu Rendern brauchen wir jedoch diese Information (schließlich könnte die Kamera auch auf dem Kopf stehen). Daher gibt es den Vektor „upDirection“ der festlegt, wo in der Szene oben sein soll. Dieser Vektor wird mit dem Einheitsvektor eY vorbelegt. Im allgemeinen ist es nicht notwendig diesen Vektor zu ändern – auch dann nicht, wenn die Kamera nach unten oder oben geneigt wird. Die Konstante „eyeDistanceToScreen“ definiert den Abstand des Auges zur Abbildungsebene. Sie entspricht der Brennweite des Kameraobjektivs. Würde man den Wert vergrößern, so würde man in die Szene hineinzoomen. Die Länge des Vektors „CamDirection“ wird, wenn die Blickrichtung der Kamera geändert wird, stets an diesen Wert angepasst.
Die Konstante „screenWidth“ definiert, wie breit die Abbildungsebene in Längeneinheiten des XYZ-Koordinatensystems ist. Wenn wir diesen Wert durch die Anzahl der Bildbreite in Pixeln dividieren, erhalten wir die Größe eines Pixels im XYZ-Koordinatensystem.
Für unsere Berechnungen benötigen wir weiterhin zwei Vektoren, welche die Abbildungsebene selbst aufspannen, also der V und W-Achse entsprechen. Wir definieren daher noch die Einheitsvektoren eV und eW, welche parallel zur V bzw. W-Achse verlaufen und die Länge 1 Pixel haben.

In der Klasse RayTraceCamera befinden sich bereits die beiden public-Methoden „MoveTo“ und „ResizeScreen“, mit denen der Ort und die Blickrichtung der Kamera sowie die Größe des zu rendernden Bitmaps geändert werden kann. Beide Methoden rufen am Ende die Methode „Init“ auf, welche die Einheitsvektoren eV und eW neu berechnet. Da der Vektor eV immer horizontal liegen soll, wird er aus dem Kreuzprodukt der Kamera-Blickrichtung und der nach-oben-Richtung gebildet.

Weitere RayTraceCamera-Methoden

Wir werden nun die RayTraceCamera um noch ein paar Methoden erweitern. Aus dem Bild zu Beginn dieses Artikels können wir entnehmen, dass wir jedem Pixel (bzw. jeder VW-Koordinate) einen Ray zuordnen können. Der Startpunkt jedes Rays ist die CamPosition. Seine Richtung ist eine Linearkombination aus der CamDirection und den Vektoren eV und eW. Die Methode „VWtoRay“ gibt den zu einer VW-Koordinate gehörenden Ray zurück:

public Ray VWtoRay(double v,double w)
{
    return new Ray(camPosition, camDirection + eV * v + eW * w);
}

Als nächstes erstellen wir die Methode „AdjustColor“. Sie bekommt eine Farbe und einen Helligkeitswert (brightness) übergeben und liefert eine neue Farbe zurück. Wenn brightness == 0 ist, entspricht die zurückgegebene Farbe genau der übergebenen Farbe. Ist brightness > 0 wird die Farbe aufgehellt, ist brightness < 0 wird sie abgedunkelt. Der Wert für brightness muß immer zwischen -1 und 1 liegen.

static Color AdjustColor(Color c, double brightness)
{
    if (brightness >= 0)
        return Color.FromArgb( // Die Farbe aufhellen
            c.R + (int)((255 - c.R) * brightness),
            c.G + (int)((255 - c.G) * brightness),
            c.B + (int)((255 - c.B) * brightness)
        );
    else // if brightness < 0
        return Color.FromArgb( // Die Farbe abdunkeln
            (int)(c.R * (1 + brightness)),
            (int)(c.G * (1 + brightness)),
            (int)(c.B * (1 + brightness))
        );
}

Die Farbe eines Pixels berechnen

Kommen wir nun zu der kompliziertesten Methode der Kamera: Die Methode „ColorAt“ soll die Farbe eines Punktes mit den Koordinaten v und w berechnen.

        static readonly double minDistToRayStart = 1E-10;

        Color ColorAt(double v, double w)
        {
            Ray ray = VWtoRay(v, w);
            PointOnPrimitive p = scene.RayTrace(ray);
            if (p == null)
                return scene.Background; // Wenn der Ray auf kein Primitiv trifft, Hintergrundfarbe der Szene zurückgeben
            else
            { // Prüfen, ob der PointOnPrimitive im Schatten liegt
                Ray rayToSun = new Ray(p.ToPointInSpace() + scene.DirectionToSun * minDistToRayStart, scene.DirectionToSun);
                if (scene.RayTraceHits(rayToSun)) return AdjustColor(p.GetColor(), scene.MaxDarkening); // Wenn keine freie Sicht auf die Sonne => Schatten

                Vector3D n = p.GetNormal(); // Muß die Länge 1 haben!
                if (n == null) return p.GetColor(); // Wenn keine Normale berechnet werden kann, Originalfarbe zurückgeben
                // Die Normale muß eine Komponente in Richtung des Betrachters haben. Sie darf nicht von ihm weg zeigen.
                if (ray.Direction * n > 0) n = n.opposite(); // Wenn das Skalaprodukt > 0 ist, ist der Winkel kleiner als 90° und wir drehen den Vektor um.

                double brightness;
                double cosAngleToLight = scene.DirectionToSun * n;

                if (cosAngleToLight > 0)
                    brightness = scene.MaxDarkening + (scene.MaxLightening - scene.MaxDarkening) * cosAngleToLight; // Es fällt Licht auf die Fläche
                else
                    brightness = scene.MaxDarkening; // Es fällt kein Licht auf die Fläche

                return AdjustColor(p.GetColor(), brightness);
            }
        }

Die Methode „ColorAt“ ermittelt zuerst mit „VWtoRay“ einen Ray, den sie mit „scene.RayTrace“ durch die Szene sendet. Wenn der Ray auf kein Primitiv trifft, kann man an dieser Stelle durch die Szene hindurch sehen, und die Hintergrundfarbe „Scene.Background“ wird zurück gegeben. Wenn der Ray auf ein Primitiv trifft, wird ein PointOnPrimitive ermittelt. Wir prüfen zunächst, ob der PointOnPrimitive im Schatten liegt, indem wir ausgehendend von seinen XYZ-Koordinaten einen neuen Ray „rayToSun“ Richtung Sonne senden. Trifft dieser Ray auf ein Primitiv, d.h. Scene.RayTraceHits(rayToSun) == true, so wird die Farbe des PointOnPrimitives maximal mit dem Wert Scene.MaxDarkening abgedunkelt und dieser Farbwert von „ColorAt“ zurückgeliefert. Es fällt auf, dass der Startpunkt von „rayToSun“ beim Erstellen des Rays ein beliebig kleines Stück der Länge minDistToRayStart in Richtung Sonne verschoben wird. Dies geschieht, damit beim Raytracen zur Sonne nicht wieder das Primitiv selbst gefunden wird und ein Primitiv sich nicht sozusagen selbst in den Schatten stellt.

Wenn der PointOnPrimitive nicht im Schatten liegt, müssen wir aus dem Winkel seiner Oberfläche und der Beleuchtungsrichtung bestimmen, wie hell dieser ist. Eine Fläche, die genau senkrecht zum Sonnenlicht steht, wird mit dem maximalen Wert „Scene.MaxLightening“ aufgehellt. Wir fragen den PointOnPrimitive zunächst mit „p.GetNormal()“ nach seinem Flächennormalenvektor „n“ (einem Vektor, der senkrecht auf der Fläche steht). Da eine Fläche zwei Seiten hat, gibt es zwei (gegenüberliegende) Richtungen, in die dieser Vektor zeigen kann. Eine dieser Richtungen hat eine Komponente in Richtung der Kamera. Die andere zeigt von der Kamera weg. Wir wollen nur die Vektorrichtung haben, welche in Richtung der Kamera zeigt. D.h. wenn der Winkel zwischen Kamerarichtung und dem Normalenvektor kleiner als 90° ist (ray.Direction * n > 0), drehen wir den Vektor mit „n.opposite()“ um.

Wir berechnen nun den Kosinus „cosAngleToLight“ aus dem Winkel zwischen dem Normalenvektor n und der Sonnenrichtung. Ist der Kosinus größer als 0 bzw. der Winkel kleiner als 90°, so fällt Licht auf die Fläche und wir berechnen aus dem Kosinus die brightness. Wenn die Fläche von der Sonne abgewendet ist (cosAngleToLight <0), fällt dagegen kein Licht darauf und wir wählen die maximale Abdunkelung „Scene.MaxDarkening“.

Das fertige Bitmap rendern

Abschließend fügen wir noch die Methode „RenderBitmap“ in die Klasse ein, welche uns eine fertige Bitmap-Grafik von der Kamera liefern soll:

        public Bitmap RenderBitmap()
        {
            int centerV = screenWidthPx / 2;
            int centerW = screenHeightPx / 2;
            var result = new Bitmap(screenWidthPx, screenHeightPx);

            Parallel.For(0, screenHeightPx, (w) =>
              {
                  for (int v = 0; v < screenWidthPx; v++)
                  {
                      Color c = ColorAt(v - centerV, centerW - w);
                      lock (result)
                      {
                          result.SetPixel(v, w, c); // ... den Pixel auf diese Farbe setzen.
                      }
                  }
              });
            return result;
        }

Wie zuvor erklärt, liegt der Nullpunkt der Abbildungsebene genau in ihrer Mitte. Daher berechnen wir zunächst seine Koordinaten „centerV“ und „centerW“, welche jeweils die Hälfte der Bildbreite bzw. -höhe betragen. Weiterhin erstellen wir ein neues Bitmap namens „result“, in das wir unsere Szene Rendern werden. Wir starten nun zwei For-Schleifen für die Koordinaten w und v, welche jeden Pixel berechnen werden. Die äußere For-Schleife wurde dabei mit „Parallel.For“ realisiert. Dies hat zur Folge, dass das .NET Framework alle Durchläufe der Schleife gleichzeitig in eigenen Threads ausführen kann. Es kann also theoretisch für jede Pixelzeile ein eigener Thread gestartet werden, was die Berechnung merklich beschleunigt.
Die Farbe des jeweiligen Pixels berechnet die Methode „ColorAt“, wobei wir die v- und w-Koordinate vor ihrem Aufruf um centerV und centerW verschieben müssen. Die Farbe weisen wir dann mit „SetPixel“ dem jeweiligen Pixel zu. Da niemals zwei Threads gleichzeitig „SetPixel“ aufrufen dürfen, wurde dieser Aufruf mit einem „lock“ abgesichert.

Damit ist die Kamera fertig!

Weiter

Jeder kennt (z.B. aus Computerspielen) die künstlichen, teilweise sogar fotorealistischen, 3D-Computergrafiken welche durch Raytracing berechnet werden. In den folgenden Beiträgen werde ich die Mathematik, die der Berechnung von 3D-Bildern zugrunde liegt, erarbeiten und einen Raytracer selbst implementieren. Natürlich gibt es bereits unzählige fertige Raytracing-Engines, die z.B. durch Hardwarebeschleunigung viel effektiver arbeiten und über sehr ausgereifte Effekte verfügen. Praktisch alle Probleme rund um das Raytracing wurden also bereits gelöst und eigentlich scheint es wenig sinnvoll das „Rad erneut zu erfinden“. Das Ziel dieses Projekts ist es daher nicht in irgend einem Aspekt besser zu sein, als bereits vorhandene Raytracer, sondern schlichtweg ein sehr tiefes Verständnis für diese Technik zu erlangen. Bei der Entwicklung des Raytracers werde ich daher vollständig auf externe Bibliotheken verzichten und alle Funktionen selbst implementieren.

Das Grundprizip

Wenn wir ein 3D-Bild auf z.B. einem Computermonitor betrachten, so sieht es so aus, als ob sich die dreidimensionale Szene hinter dem Monitor befinden würde. Der Monitor selbst erscheint uns wie ein Fenster, durch das wir die Szene betrachten. In Wirklichkeit besteht das Bild auf dem Monitor natürlich aus einzelnen Pixeln, von denen jedes Pixel eine andere Farbe hat. Die einzelnen Pixelfarben möchten wir berechnen.

Wir möchten also das Bild einer dreidimensionalen Szene (hier: zwei Kugeln) auf einer Abbildungsebene (Monitor), welche sich zwischen dem Auge des Betrachters und der Szene befindet, berechnen. Dazu berechnen wir ausgehend von dem Auge einen Strahl durch jeden einzelnen Pixel im Pixelgitter der Abbildungsebene und verfolgen den Strahl so lange durch die Szene, bis er auf ein Objekt stößt. Die Farbe dieses Objekts ist dann die Farbe des jeweiligen Pixels.

Um einen solchen Strahl zu beschreiben definieren wir zunächst die Klasse Ray:

    public class Ray
    {
        public Vector3D Start { get; private set; }
        public Vector3D Direction { get; private set; }

        public Ray(Vector3D start, Vector3D direction)
        {
            this.Start = start; this.Direction = direction.normalize();
        }
    }
}

Ein Ray besteht also aus zwei Vektoren. Seiner Startposition (hier dem Auge des Betrachters) und seiner Richtung. Die Klasse Vector3D habe ich hier beschrieben. Der Richtungsvektor „Direction“ wird im Konstruktor eines Rays normalisiert. Er hat also immer die Länge 1.

Die Szene, Objekte und Primitive

Als Szene bezeichnen wir die Menge aller geometrischen Objekte, welche durch unseren Raytracer auf die Abbildungsebene abgebildet werden sollen. Ein Objekt (z.B. ein Haus, ein Baum, etc.) besteht im Allgemeinen aus vielen kleinen Primitiven. Ein Primitiv (z.B. ein Dreieck oder Viereck) ist ein elementarer Baustein einer Szene, der vom Raytracer direkt verarbeitet werden kann. Alle aufwändigeren Objekte (Häuser, etc.) müssen aus vielen kleinen Primitiven zusammengesetzt werden.

Definieren wir zunächst die abstrakte Klasse Primitive, von der später alle konkreten Primitive (Dreiecke, Vierecke, etc.) abgeleitet werden:

    abstract public class Primitive
    {
        public Color color { get; private set; }
        public abstract PointOnPrimitive RayTrace(Ray ray);

        public Primitive(Color color)
        {
            this.color = color;
        }

    }

Jedes Primitiv muss eine Farbe haben. Deshalb muss diese bereits beim Konstruktoraufruf angegeben werden. Weiterhin verfügt jedes Primitiv über eine Methode namens RayTrace, welche beim Aufruf einen Ray als Parameter erhält. In dieser Methode berechnet das Primitiv, ob der Ray seine Oberfläche schneidet. Ist dies nicht der Fall, wird null zurückgegeben. Gibt es einen Schnittpunkt, wird ein PointOnPrimitive zurückgegeben. Dieses Objekt beschreibt einen Schnittpunkt zwischen einem Ray und einem Primitiv.

Die abstrakte Klasse PointOnPrimitive sieht wie folgt aus:

    abstract public class PointOnPrimitive
    {
        public double distanceToRayStart { get; private set; }
        public abstract Vector3D ToPointInSpace();
        public abstract Color GetColor();
        public abstract Vector3D GetNormal();
        public abstract Primitive GetPrimitive();

        public PointOnPrimitive(double distanceToRayStart)
        {
            this.distanceToRayStart = distanceToRayStart;
        }
    }

Je nachdem, um was für ein Primitiv es sich handelt, kann es verschiedene Implementierungen dieser abstrakten Klasse geben, um die wir uns später kümmern. Schauen wir uns zunächst die Methoden dieser Klasse an:

Die Methode ToPointInSpace() berechnet die Position des PointOnPrimitive im Raum, d.h. seine X, Y und Z Koordinate, und gibt diesen als Vector3D zurück. Dieser Punkt hat einen Abstand von vom Startpunkt des Rays (bzw. des Beobachters), welchen wir mit distanceToRayStart abfragen können. Wenn wir alle Schnittpunkte eines Rays mit allen Primitiven in der Szene berechnen, so wird der Ray in der Regel mehrere Primitive schneiden. Für die Farbe des Pixels auf der Abbildungsebene ist nur der erste Schnittpunkt mit einem Primitiv von Bedeutung, da alle hinteren Primitive von dem vorderen Primitiv verdeckt sind. Finden wir also zu einem Ray mehrere PointOnPrimitives, so müssen wir nur den PointOnPrimitive mit dem geringsten distanceToRayStart verwenden. Mit GetColor() können wir die Farbe des Primitivs, auf dem der PointOnPrimitive liegt, abfragen. Mit GetPrimitive() erhalten wir das Primitiv selbst.

Die Helligkeit eines PointOnPrimitive hängt von dem Winkel zwischen dem Lichteinfall und der Oberfläche des Primitivs ab, denn eine Fläche, die quer zum einfallenden Licht steht, ist wesentlich heller, als eine Fläche, die vom Licht nicht angestrahlt wird. Um herauszufinden, wie die Fläche, auf dem der PointOnPrimitive liegt, geneigt ist, verwenden wir die Methode GetNormal(). Sie liefert uns einen Normalenvektor zu der Ebene, also einen Vektor, der genau senkrecht auf der Primitivoberfläche steht.

Zurück zur Szene:

Die Szene ist also unser Raum, in dem sich alle Primitive befinden. Zusammen bilden die Primitive z.B. eine Landschaft mit Häusern, Bäumen, etc. Aus Entwicklersicht ist eine Szene etwas, in dem wir Raytracen können. Wir definieren daher nun das Interface IRayTraceable. Jedes Objekt, welches dieses Interface implementiert, repräsentiert also einen Raum mit Primitiven, durch den wir Strahlen bzw. Rays senden können. Ein Ray trifft dabei entweder auf ein Primitiv oder er passiert den Raum ungehindert.

Das Interface IRayTraceable sieht wie folgt aus:

    public interface IRayTraceable
    {
        Vector3D DirectionToSun { get; set; }
        Color Background { get; set; }
        double MaxLightening { get; set; } // Gültige Werte von 0 (Originalfarbe) bis 1 (jede Farbe wird bis auf Weiss aufgehellt)
        double MaxDarkening { get; set; } // Gültige Werte von 0 (Originalfarbe) bis -1 (jede Farbe wird bis auf Schwarz abgedunkelt)
        PointOnPrimitive RayTrace(Ray ray);
        bool RayTraceHits(Ray ray); // Liefert true, wenn der Ray auf ein beliebiges Primitive trifft.
    }

Jede Szene braucht eine Lichtquelle, damit für unterschiedliche Ausrichtungen von Oberflächen unterschiedliche Farben bzw. Helligkeitswerte berechnet werden können. Würde eine Lichtquelle fehlen, dann würde eine Kugel aussehen wie ein flacher einfarbiger Kreis und der dreidimensionale Eindruck ginge verloren. Eine Kugel wirkt erst durch die unterschiedlichen Helligkeits-Schattierungen dreidimensional. Um die Szene nach ihrer Beleuchtungsrichtung zu fragen, gibt es in dem Interface den Vektor „DirectionToSun“. Je nachdem in welchem Winkel das Licht auf eine Oberfläche fällt, wird diese ausgehend von ihrer Originalfarbe aufgehellt oder abgedunkelt. Mit „MaxDarkening“ wird die maximale Abdunkelung einer Oberfläche festgelegt. Ist dieser Wert auf -1, so sind alle Flächen, auf die kein Sonnenlicht fällt absolut schwarz. Wird der Wert größer gewählt (z.B. -0,5) so gibt es ein diffuses Umgebungslicht in der Szene, welches die Abdunkelung begrenzt. Mit „MaxLightening“ wird festgelegt, wie intensiv die Sonneneinstrahlung ist. Wird der Wert auf 1 gesetzt, so ist jede Oberfläche die senkrecht zur Sonnenstrahlung steht, absolut weiß. Wird ein kleinerer Wert gewählt (z.B. 0.8), so wird die Farbe nicht ganz so weit aufgehellt. Einige Rays werden beim Raytracen die Szene passieren, ohne auf ein Primitiv zu treffen. Diese Pixel werden in der Farbe „Background“ des Interfaces dargestellt.

Die Methoden „RayTrace“ und „RayTraceHits“ dienen dazu Strahlen durch die Szene zu senden. Der Strahl bzw. Ray selbst wird als Parameter übergeben. Trifft dieser Ray auf ein Primitiv, so gibt die Methode „RayTrace“ einen PointOnPrimitive zurück, welcher den Schnittpunkt zwischen Ray und Primitiv beschreibt. Trifft der Ray auf kein Primitiv, so wird null zurückgegeben. Die Methode RayTraceHits arbeitet sehr ähnlich. Sie gibt jedoch nur den Wert true wenn der Ray auf ein beliebiges Primitiv trifft, und false wenn der Ray die Szene ungehindert passiert.

Mit diesen Interfaces bzw. abstrakten Klassen haben wir bereits alle wichtigen Schnittstellen in unserem Raytracer beschrieben. In den folgenden Beiträgen werden wir die einzelnen konkreten Klassen, welche diese Schnittstellen verwenden, implementieren.

Weiter

Wer Software entwickelt, die geometrische Berechnungen durchführt, kommt meist nicht drum herum sich erneut mit der aus der Schulzeit bereits bekannten Vektorrechnung zu beschäftigen. Die im Folgenden vorgestellte Klasse Vector3D macht uns das Leben etwas einfacher. Ein Objekt dieser Klasse repräsentiert einen dreidimensionalen Vektor und alle gängigen Vektoroperationen sind bereits implementiert.

Hier sind einige Anwendungsbeispiele:

            // Zwei neue Vektoren erstellen:
            Vector3D V = new Vector3D(1, 3, 4);
            Vector3D W = new Vector3D(2, 1, 5);

            // Die Vektoren addieren, subtrahieren und multiplizieren:
            Vector3D sum = V + W;
            Vector3D diff = V - W;
            double s = V * W; // Skalarprodukt berechnen
            Vector3D k = V.cross(W); // Kreuzprodukt berechnen
            Vector3D V_resize = V * 2.5; // Vektor mit Skalar multiplizieren

            // Die Länge eines Vektors berechnen:
            double V_length = V.length();

            // Einen Vektor normalisieren (d.h. seine Länge auf 1 ändern):
            Vector3D V_normalized = V.normalize();

            // Gegenvektor berechnen (d.h. mit -1 multiplizieren):
            Vector3D V_opposite = V.opposite();

            // Prüfen, ob zwei Vektoren parallel sind:
            if(V.isCollinearTo(W))
            {
                Console.WriteLine("V und W sind parallel!");
            }

In der Klasse Vector3D gibt es noch einige weitere Methoden, z.B. um einen Vektor zu drehen oder auf eine Ebene oder einen anderen Vektor zu projizieren. Diese Methoden werden durch Kommentare im Quelltext erklärt.

Die Klasse Vektor3D:

    public class Vector3D
    {
        public double X { get; private set; }
        public double Y { get; private set; }
        public double Z { get; private set; }

        // Einheitsvektoren:
        public static readonly Vector3D eX = new Vector3D(1, 0, 0);
        public static readonly Vector3D eY = new Vector3D(0, 1, 0);
        public static readonly Vector3D eZ = new Vector3D(0, 0, 1);
        public static readonly Vector3D Zero = new Vector3D(0, 0, 0);

        public Vector3D(double _x, double _y, double _z)
        {
            X = _x; Y = _y; Z = _z;
        }

        public static Vector3D operator +(Vector3D v, Vector3D w)
        {
            return new Vector3D(v.X + w.X, v.Y + w.Y, v.Z + w.Z);
        }

        public static Vector3D operator -(Vector3D v, Vector3D w)
        {
            return new Vector3D(v.X - w.X, v.Y - w.Y, v.Z - w.Z);
        }

        public static double operator *(Vector3D v, Vector3D w)
        {
            return v.X * w.X + v.Y * w.Y + v.Z * w.Z;
        }

        public static Vector3D operator *(Vector3D v, double w)
        {
            return new Vector3D(v.X * w, v.Y * w, v.Z * w);
        }

        public Vector3D cross(Vector3D w) // Kreuzprodukt (this x W)
        {
            return new Vector3D(Y * w.Z - Z * w.Y, Z * w.X - X * w.Z, X * w.Y - Y * w.X);
        }

        public double length()
        {
            return Math.Sqrt(X * X + Y * Y + Z * Z);
        }

        public Vector3D normalize()
        {
            double L = length();
            return new Vector3D(X / L, Y / L, Z / L);
        }

        public Vector3D opposite()
        {
            return new Vector3D(-X, -Y, -Z);
        }

        public void assertNormal()
        {
            double l = length();
            if (l < 0.9999 || l > 1.0001) throw new Exception("Vector3D is not normalized!");
        }

        public bool isCollinearTo(Vector3D w)
        {
            double sp = this * w;
            double l = this.length() * w.length();
            return Math.Abs(sp - l) < 0.0001 || Math.Abs(sp + l) < 0.0001;
        }

        public override string ToString()
        {
            return "(" + X.ToString("F2") + "; " + Y.ToString("F2") + "; " + Z.ToString("F2") + ")";
        }

        public static double matrixDet(Vector3D a, Vector3D b, Vector3D c)
        {
            return a.X * b.Y * c.Z + b.X * c.Y * a.Z + c.X * a.Y * b.Z
                 - a.Z * b.Y * c.X - b.Z * c.Y * a.X - c.Z * a.Y * b.X;
        }

        public static bool cramer(Vector3D A, Vector3D B, Vector3D C, Vector3D Sum, out double a, out double b, out double c)
        { // Löst das LGS a*A + b*B +c*C = Sum. Wenn es keine Lösung gibt wird false zurück gegeben.
            double det = Vector3D.matrixDet(A, B, C);
            if (det == 0) { a = 0; b = 0; c = 0; return false; }
            a = Vector3D.matrixDet(Sum, B, C) / det;
            if (Double.IsNaN(a)) { b = 0; c = 0; return false; }
            b = Vector3D.matrixDet(A, Sum, C) / det;
            if (Double.IsNaN(b)) { c = 0; return false; }
            c = Vector3D.matrixDet(A, B, Sum) / det;
            if (Double.IsNaN(c)) return false;
            return true;
        }

        public Vector3D projectOnPlane(Vector3D planeNormal)
        { // Projiziert den Vektor auf die Ebene senkrecht zu planeNormal, bzw. entfernt die Komponente in planeNormal-Richtung aus dem Vektor.
            planeNormal = planeNormal.normalize();
            return this - planeNormal * (planeNormal * this);
        }

        public Vector3D projectOnVector3D(Vector3D vec)
        {// Projeziert den Vektor auf vec, bzw. gibt nur seine Komponente in vec-Richtung zurück.
            vec = vec.normalize();
            return vec * (this * vec);
        }

        public Vector3D rotateAround(Vector3D startPoint, Vector3D axis, double angle)
        { // Rotiert den durch this beschriebenen Punkt um die Gerade mit Stützpunkt startPoint und Richtung axis. Bei Blickrichtung in axis-Richtung wird der Punkt bei positivem angle im Uhrzeigersinn rotiert.
            axis = axis.normalize();
            Vector3D V = (this - startPoint).projectOnPlane(axis); // Vektor von Gerade (Projektionspunkt) zu this, senkrecht zu axis
            Vector3D W = axis.cross(V).normalize() * V.length();  // W= V um 90° im Uhrzeigersinn weiter gedreht.
            double a = (this - V - startPoint).length(); // Abstand von startPoint zum Projektionspunkt von this auf die Gerade.
            return startPoint + (axis * a) + V * Math.Cos(angle) + W * Math.Sin(angle);
        }

        double angle(Vector3D P1, Vector3D P2)
        { // Berechnet den Winkel zwischen den Punkten P1 und P2 am Punkt this in Radiant
            Vector3D V1 = (P1 - this);
            Vector3D V2 = (P2 - this);
            return Math.Acos(V1 * V2 / (V1.length() * V2.length()));
        }
    }